写在前面
这个东西其实是有价值的东西。因为在软体模拟、数学方程可视化、流体模拟、数据可视化等等方面都有其用武之地。
如水的模拟：
心形函数方程转图像
线性报表
其原理都是通过三次贝塞尔曲线将有限个数的点平滑化。
问题建模
已知若干个点，绘制出该点连接的曲线。
|
1 2 3 4 5 6 7 8 |
<canvas width="480" height="480"></canvas> <script> function drawPath(path){ //实现 } drawPath([{ x: 50, y: 50 }, { x: 200, y: 100 }, { x: 250, y: 50 }, { x: 350, y: 150 }, { x: 370, y: 100 }, { x: 570, y: 200 }]) </script> |
这里实验平台使用浏览器环境，即 Canvas 相关 API 以及 javascript 语言。
这里 canvas 的上下文对象拥有了 bezierCurveTo 方法，故免去了自己实现 bezierCurveTo 的一些事情。
|
1 |
context.bezierCurveTo(cp1x,cp1y,cp2x,cp2y,x,y); |
实现图解
实现目标
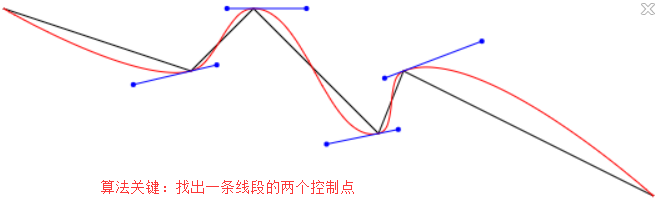
具体过程
代码
Vector2，一般用来表示向量，但有的时候也用来当作点来进行一计算。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
var Vector2 = function(x, y) { this.x = x; this.y = y; } Vector2.prototype = { "length": function () { return Math.sqrt(this.x * this.x + this.y * this.y); }, "normalize": function () { var inv = 1 / this.length(); return new Vector2(this.x * inv, this.y * inv); }, "add": function (v) { return new Vector2(this.x + v.x, this.y + v.y); }, "multiply": function (f) { return new Vector2(this.x * f, this.y * f); }, "dot": function (v) { return this.x * v.x + this.y * v.y; }, "angle": function (v) { return Math.acos(this.dot(v) / (this.length() *v.length())) * 180 / Math.PI; } } |
其中
length 求向量长度
normalize 转单位向量
add 向量叠加
multiply 向量翻倍
dot 内积
angle 方法用来求两个向量的夹角
核心方法，根据 path 上的点，求出所有贝塞尔曲线控制点。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
function getControlPoint(path) { var rt = 0.3; var i = 0, count = path.length - 2; var arr = []; for (; i < count; i++) { var a = path[i], b = path[i + 1], c = path[i + 2]; var v1 = new Vector2(a.x - b.x, a.y - b.y); var v2 = new Vector2(c.x - b.x, c.y - b.y); var v1Len = v1.length(), v2Len = v2.length(); var centerV = v1.normalize().add(v2.normalize()).normalize(); var ncp1 = new Vector2(centerV.y, centerV.x * -1); var ncp2 = new Vector2(centerV.y * -1, centerV.x); if (ncp1.angle(v1) < 90) { var p1 = ncp1.multiply(v1Len * rt).add(b); var p2 = ncp2.multiply(v2Len * rt).add(b); arr.push(p1, p2) } else { var p1 = ncp1.multiply(v2Len * rt).add(b); var p2 = ncp2.multiply(v1Len * rt).add(b); arr.push(p2, p1) } } return arr; } |
戴文奇 2015 年 8 月 26 日
最终的步骤 对两个单位法向量 b 和 c 求控制点， 为什么缩放系数是 e 和 f 的模 乘以写死的 0.3？？ 为什么是 0.3？怎么不是 0.4？
TAT.dnt 2015 年 8 月 26 日
问得好！这个值决定了控制点在 b 或者 c 方向上的长度，长度越长，拉伸的力度越大，曲线的弯曲也越大。0.3 是一个非常合适的值，当然这个也可以根据个人审美喜好进行调节，总之，这个系数决定了弯曲程度。
戴文奇 2015 年 8 月 26 日
thanks~