与 A-Star 不同的像素级寻路算法上

In 未分类 on 2016年03月04日 by TAT.vorshen view: 4,697

前言：

寻路是游戏中非常重要的一项功能，这项功能将直接体现出 AI 的智商如何。那说起寻路的算法，就不得不提标题上面的 A star 算法了。A Star（又称 A*），是结合了 Dijkstra 算法和贪心算法优点的算法，对此不了解的同学可以去搜索一下，这里不具体介绍实现，而是简单的说一下原理，为后面我们的主角铺垫。

A Star 的核心在于将游戏背景分为一个又一个格子，每个格子有自己的靠谱值，然后通过遍历起点的格子去找到周围靠谱的格子，接着继续遍历周围…… 最终找到终点。好了，A Star 的介绍就到这里了，因为它不是文章的主角。

文章篇幅较长所以分为上下文，下文地址：

上下文各有一种实现方式，区别看了就知道，此外上文包含了一些研究寻路的思考。

开头介绍 A Star 我们提及了格子，这是 A Star 最核心的一个地方，不过并不是所有游戏都引入了格子的概念，还有很多的游戏是像素级别的。虽然说像素也是一个个的格子，如果用 A Star 针对像素来寻路，试想如果一个 1366*768 分辨率的屏幕，那格子的总数将会有 1049088 个，这明显是很不合适的。

那么接下来就有请我们的文章主角出场了，算法没有名字，因为百分百原创，可能还有一些自己没有发现的坑点，希望和大家一起讨论研究~

1、寻路的本质是什么

在现实生活中寻路就是从起点到达目的地，在游戏中也是如此，区别在于我们人在现实中会自己避开各个障碍物，而计算机不会，所以寻路本质就是我们帮助计算机避开一个又一个障碍物

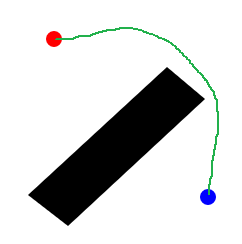
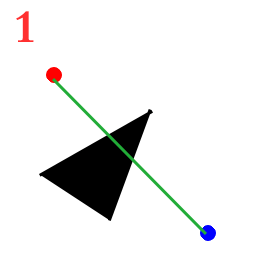
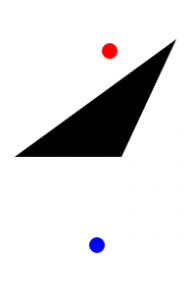
如果我们对计算机下达一个从红点到蓝点的命令，如图

第二幅图中我们必须要帮助计算机绕开多边形

2、该以怎么样的方式绕开

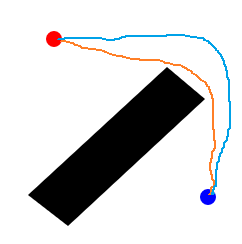
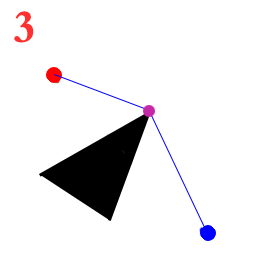
下图中红线和蓝线都是绕开的表现，但所有人都不会选择蓝色的方式，因为它远

远的路径有很多很多，那么什么是最近的呢，我们知道：两点之间，线段最短

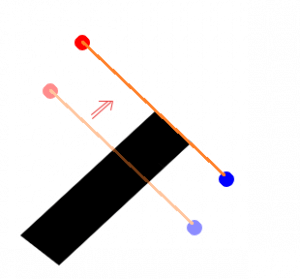
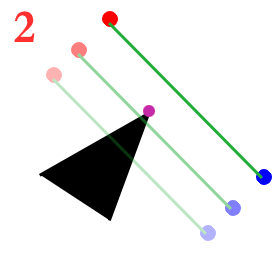
但我们用最短路径的话一定与障碍物多边形相交，这时候我们换一种思维，不考虑绕过，而考虑什么时候不会相交，如图

看！只要将起点终点平移了就没有相交了！

先别慌着喷我…… 看下图

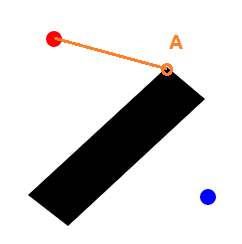
这里 A 点我称之为必过点，就是以最短绕开路径一定会经过的点，①

我们刚刚通过平移移动起点和终点的绝对位置，不改变它们相对位置，扫过了障碍物区域，发现了一个必过点

整个寻路的思想就是如此！

接下来说具体在程序中是如何实现的

a、先将起点终点连接

b、针对连线的垂直平分线方向平移

c、直到发现连线没有与障碍物相交即可

d、去障碍物上与那个没有相交的线最近点 (也就是必过点)，分别与起点和终点相连

整个流程就是如此，下面说实现过程中的一些难点和坑点

1、如何找到必过点

因为我们所说的连线与障碍物相交，本质上是与障碍物中的某一条线相交了

图中蓝线和红线相交所以说与障碍物相交了

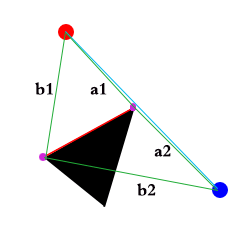
我们找必过点的方式就是首先找到连线最后相交的障碍物的两点，然后针对这两点分别求到起点和终点的距离

就是图中比较 a1+a2 和 b1+b2 的大小，距离小的就是必过点

2、第一次找到的必过点无法直接和终点或起点相连

这个就是用核心思想递归的再去找下一个必过点

不过代码里面我是用循环做的

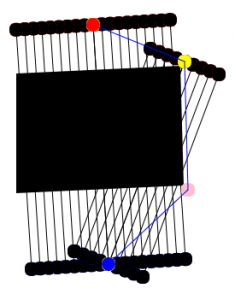
给出一张开启 debug 的演示图

那么多黑点黑线是平移的轨迹，然后黄点是第一个必过点，此时发现黄点无法与蓝色点相连，那么 continue，以黄点为起点和蓝点为终点，找出第二个必过点粉色的点

3、平移连线穿过必过点，大坑

注意小标题中的穿字，先用一个例子表示出来

开启 debug 我们走一遍看看~

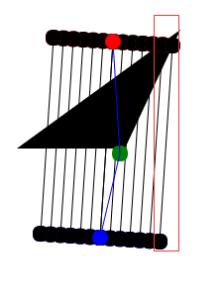
注：我这里设定了只找一个必过点，所以出现了穿越的情况

但问题是怎么必过点（绿点）会出现在这儿！！

因为那个红框，平行线（红框内的那个）过了障碍物没问题，但它是穿越过去的！不是按我们想的横扫过去的！

那该如何解决，这时候就需要我们矫正起点和终点了

只需要把起点和终点都保证在障碍物的 AABB 外就可以了，AABB 就是将一个多边形看成长方形，它的 x，y，width 和 height

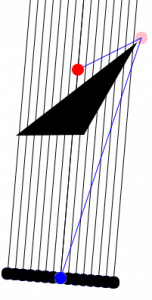
这个在 AABB 外也不是随便取得，必须按照连线的方向去延长，让我们看看效果

如图所示

在线演示地址：http://westanhui.github.io/navigate/index.html

注意：点击画障碍物，通过左键单击画多边形最后右键自动闭合图像

下面贴核心代码和解释（完整代码可查看页面源代码）

function determinant(a, b, c, d) {

return (a * d - b * c);

}

function isLineCross(a1, a2, b1, b2) {

if(globalIndex++ > 1000) {

throw 'to much times';

}

var delta = determinant(a2.x - a1.x, b1.x - b2.x, a2.y - a1.y, b1.y - b2.y);

if(delta <= (1e-6) && delta >= -(1e-6)) {

return false;

}

var namenda = determinant(b1.x - a1.x, b1.x - b2.x, b1.y - a1.y, b1.y - b2.y) / delta;

if(namenda > 1 || namenda < 0) {

return false;

}

var miu = determinant(a2.x - a1.x, b1.x - a1.x, a2.y - a1.y, b1.y - a1.y) / delta;

if(miu > 1 || miu < 0) {

return false;

}

return true;

}

这个是工具方法，判断两条线是否相交的，用的是矩阵的方法

// 首先判断起点终点是不是在障碍物内

var outPoint = getPointOutside(obstacles);

if(isInObstacles(outPoint, start, obstacles)) {

alert('fuck');

return ;

}

if(isInObstacles(outPoint, end, obstacles)) {

alert('fuck');

return ;

}

function isInObstacles(start, end, obstacles) {

var index = 0;

var result;

for(var i = 0; i < obstacles.length - 1; i++) {

result = isLineCross(start, end, obstacles[i], obstacles[i + 1]);

if(result) {

index++;

}

index = index % 2;

if(index === 0) {

return false;

} else {

return true;

}

这个用了经典的射线法去判断某个点是否在一个多边形内

原理就是在多边形外面取一点，然后和判断的点相连，与多边形相交个数为偶数则点不在多边形内，为奇数则在多边形内

// 计算斜率

k = (end.y - start.y) / (end.x - start.x); // 连线的斜率

kk = -1 / k; // 连线的垂直平分线的斜率

// 判断起点终点是否在障碍物的AABB内

limit = getAABB(obstacles);

// 矫正位置

var currStart = redressPoint(start, end, limit);

var currEnd = redressPoint(end, start, limit);

function redressPoint(aPoint, bPoint, limit) {

var tmpX;

var tmpY;

var tmpPoint;

if(isInAABB(aPoint, limit)) { // 如果点在障碍物的AABB内就矫正位置

if(bPoint.x > aPoint.x) { // 计算两点x的相对位置，这里先以x来偏移y

tmpX = limit.minX; // 如果a点x小于b点，那么就默认移动到AABB中最小的x点位置

tmpY = aPoint.y - (aPoint.x - tmpX) * k; // 根据斜率算y的偏移

} else { // 与上同理

tmpX = limit.maxX;

tmpY = aPoint.y - (aPoint.x - tmpX) * k;

}

tmpPoint = {

x: tmpX,

y: tmpY

};

if(tmpY < limit.maxY && tmpY > limit.minY) { // 根据刚刚矫正偏移的x，y判断是否出了AABB，没有则以y为基准偏移x重新矫正

if(bPoint.y > aPoint.y) {

tmpY = limit.minY;

tmpX = aPoint.x - (aPoint.y - tmpY) / k;

} else {

tmpY = limit.maxY;

tmpX = aPoint.x - (aPoint.y - tmpY) / k;

}

tmpPoint = { // 该点就是矫正点

x: tmpX,

y: tmpY

};

}

} else {

tmpPoint = aPoint; // 无须矫正

}

if(isDebug) { // debug模式下显示矫正的点在哪

drawCircle(tmpPoint, 'yellow');

}

return tmpPoint;

}

这里是矫正起点终点的代码，其中主要都是关于斜率的数学计算，感兴趣的同学可以走一遍看看，注意其中先是按 x 为基准根据斜率算出矫正后的 y，得到新的 (x,y)，然后判断这个点是否出了障碍物的 AABB，没有的话重新按 y 为基准去算 x，两种情况肯定有一种会将点矫正出障碍物的 AABB

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

157

158

159

160

161

162

163

164

165

function check(start, end, obstacles) {

var isCollision = true; // 结束判断符

var dir = 0; // 方向

isBodyCross(start, end, obstacles);

function isBodyCross(currStart, currEnd, obstacles) {

var unit = 50; // 每次平移的基数单位

var index = 0; // 偏移的次数

var changeX = 0; // 平移x方向的具体改变量

var changeY = 0; // 平移y方向的具体改变量

var door1 = true;

var door2 = true;

k = (currEnd.y - currStart.y) / (currEnd.x - currStart.x); // 连线的斜率

kk = -1 / k; // 连线的垂直线的斜率

if(Math.abs(k) > 1) { // 以x为单位的变动

changeX = 10;

changeY = 10 * kk;

} else { // 以y为单位的变动

changeX = 10 / kk;

changeY = 10;

}

while(isCollision) { // 当不碰撞的时候结束循环

if(index > 1000) { // 增加一个界限

alert('Error');

return ;

}

// 开始某个方向的寻路

door1 = true;

nextStart = {

x: currStart.x + changeX * index,

y: currStart.y + changeY * index

};

nextEnd = {

x: currEnd.x + changeX * index,

y: currEnd.y + changeY * index

};

for(var i = 0; i < obstacles.length - 1; i++) {

result = isLineCross(nextStart, nextEnd, obstacles[i], obstacles[i + 1]);

if(result) { // 连线碰撞

x1 = obstacles[i]; // 最后碰撞边上的点

y1 = obstacles[i + 1]; // 最后碰撞边上的点

door1 = false;

drawRole(nextStart, nextEnd);

break;

}

if(door1) { // 没有阻碍

dir = 1;

isCollision = false;

break;

}

// 另一个方向的寻路

door2 = true;

nextStart = {

x: currStart.x - (changeX * index),

y: currStart.y - (changeY * index)

};

nextEnd = {

x: currEnd.x - (changeX * index),

y: currEnd.y - (changeY * index)

};

for(i = 0; i < obstacles.length - 1; i++) {

result = isLineCross(nextStart, nextEnd, obstacles[i], obstacles[i + 1]);

if(result) {

x2 = obstacles[i];

y2 = obstacles[i + 1];

door2 = false;

drawRole(nextStart, nextEnd);

break;

}

if(i === obstacles.length - 1) { // 检测完障碍物上的边，没有碰撞

dir = -1;

isCollision = false;

break;

}

index++;

}

if(door1 || door2) {

fixPoint(changeX, changeY); // 确定必过点

}

function fixPoint(changeX, changeY) {

var dis1;

var dis2;

var f;

var x, y;

if(dir === 1) {

x = x1;

y = y1;

} else {

x = x2;

y = y2;

}

if(typeof x === 'undefined') {

return ;

}

// 算距离

dis1 = distance(x, nextStart, nextEnd);

dis2 = distance(y, nextStart, nextEnd);

var symbolX;

var symbolY;

if(dis1 < dis2) { // 比较距离的大小，得出必过点，此时x是必过点

// 下面两个if用来将必过点往整个障碍物外面偏移一点

if(x.y > y.y) {

symbolY = 1;

} else {

symbolY = -1;

}

if(x.x > y.x) {

symbolX = 1;

} else {

symbolX = -1;

}

f = { // 偏移后的必过点

x: x.x + (5 * symbolX),

y: x.y + (5 * symbolY)

};

drawCircle(f, 'green');

} else { // 必过点是y

if(y.y > x.y) {

symbolY = 1;

} else {

symbolY = -1;

}

if(y.x > x.x) {

symbolX = 1;

} else {

symbolX = -1;

}

f = { // 最终必过点的位置

x: y.x + (5 * symbolX),

y: y.y + (5 * symbolY)

};

drawCircle(f, 'pink');

}

// 将必过点添加到最终路径

f.index = end.index;

globalPath.splice(f.index, 0, f);

for(var i = 0; i < globalPath.length; i++) {

globalPath[i].index = i;

}

// 下一轮计算前这些值设置为undefined

x1 = undefined;

y1 = undefined;

x2 = undefined;

y2 = undefined;

var tmp = redressPoint(globalPath[f.index - 1], f, limit); // 矫正

check(tmp, f, obstacles);

tmp = redressPoint(globalPath[f.index + 1], f, limit); // 矫正

check(f, tmp, obstacles);

}

核心的代码，先看外面的 dir，它是方向，因为这个平行是要按照两个方向去判断的

unit 值的大小决定平移的精度，我自己用的是 50px，感觉还不错，如果这个值过大，可能会出现跳过障碍物某条边的情况，如果这个值过小，会影响性能

changeX 和 changeY 是 x 方向和 y 方向变动的值，根据斜率计算出来的

然后 while 循环就开始不停的找到每一个必过点，而确定必过点就是通过 fixPoint 函数，dis1 和 dis2 是用来计算长度判断一个边上的两个点哪个是必过点，前面有说过。symbolX 和 symbolY 是当时有些画蛇添足的一步，用来把找到的必过点向外偏移一点，方便看清楚，看 demo 效果挺好，不过实际上是不需要的

—————————————————— 我是分隔符————————————————————

说了这么多，也贴出了在线演示地址，简单易操作，就不说了，下面说一下这个方法不足的地方

有一个不足，但也是一个很致命的不足，就是一旦起点或者终点就在障碍物的 AABB 内，而且这个 AABB 内很怪异的时候，会出现问题，下面举出例子

一旦起点或者终点被障碍物这样诡异的包围的时候，整个寻路就会出现问题，即使我们将点矫正出障碍物的 AABB 也不行

原因的本质是我们的算法核心是连线平移去绕过障碍物，只要出现连线平移穿过障碍物的情况那就违背绕的本质

有问题我们自然要解决

我尝试了一些方法，比如分割障碍物，多次矫正等等，都不合适，本身算法核心的问题再怎么 hack 也没办法

那怎么办，看之前标注的①，我们将关注点由连线变成多边形上的每个点，因为每个点都可能是必过点不是么~

下文会详细讲解另外一种方法

最后：

既然该方法有致命的弱点，那它能用吗？

我认为是可以的，但有一定的条件，就是重点和起点尽量不要在障碍物的 AABB 内，障碍物不是多边形也没事，这是该方法优势的一个情况，目前我们的障碍物都是多边形，如果是圆呢？因为该方法考虑的是起点和终点的连线，对障碍物几乎没有要求，只需要根据平行后的连线算出必过点就可以了，所以对障碍物形状没有要求，只有对位置有一定的要求

好了，这篇文章就说到这儿了，下篇文章我们将以另一个角度去寻路，无视起点终点被诡异的障碍物包裹

请看下文：

http://www.alloyteam.com/2016/03/with-a-star-under-different-pixel-pathfinding-algorithm/

原创文章转载请注明：

转载自AlloyTeam：http://www.alloyteam.com/2016/03/and-a-star-on-different-pixel-pathfinding-algorithm/

分享到:

AlloyTeam

AlloyTeam

发表评论