先贴上文地址:http://www.alloyteam.com/2016/03/and-a-star-on-different-pixel-pathfinding-algorithm/
之前说到了起点和终点连线平移方式的不足,那这篇文章就介绍另一个给力的方法
演示地址:
http://westanhui.github.io/navigate/index2.html
注意:点击画障碍物,通过左键单击画多边形最后右键自动闭合图像
上文中我们绕过障碍物的核心是起点和终点的连线扫过障碍物,当障碍物为多边形的时候,扫过障碍物一定意味着最后是扫过了障碍物上的某一个点
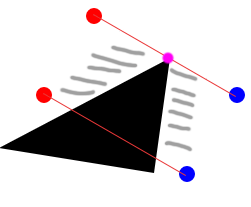
那么这一点也一定能成为必过点,那我们就先尽可能的找到每一个点,把它当成必过点来看
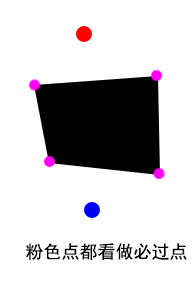
然后我们把“ 这些必过点尽可能的相连起来,再与起点和终点相连起来,从里面找出最短的一条路径来”,这是整个寻路的核心,已经用语言描述了出来,下面是用程序表现的一些问题
1、哪些点可能成为我们的必过点,不可能所有的点都是的,比如下图
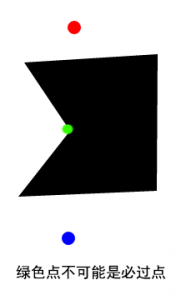
在这里我的判断方法是取起点或终点中的一点,然后找到障碍物上能和其直接相连的点(1 级点,不止一个)
然后遍历这些 1 级点,找到障碍物中可以直接相连的 2 级点们…… 以此内推,一直找到某一个点可以直接与终点相连
对,就是树的思想!
2、哪些点是被算作为可直接相连的
这个对于人眼看来很容易区分,但对于计算机稍微有些麻烦
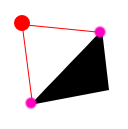


图中红色的连线都算作可以直接相连,而下面这样的则不算做相连
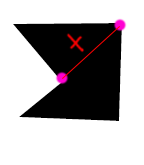
程序中的判断一定要考虑周全
3、择优取点
之前说了整个核心是树的思想,不停的找某个点的下级可行直连点,什么是可行直连点,请点击下面 gif 图
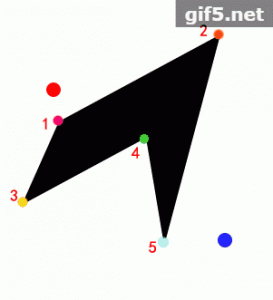
看下图中障碍物上标了数字的点
由起点出发,起点的直连点有三个,1,2,3
然后我们来看 3 点的直连点有哪些,图中轻易可知有四个,起点、1,、4、5 这几个点
哪些被算作可行直连点呢,起点不可以,因为它是 3 点的父级点,1 也不可以,它是 3 点的兄弟节点
所以在这里我们认为 4 点和 5 点是 3 点的可行直连点,同理可以得到 5 点的可行直连点只有终点
再用一个树的结构图来表示一下
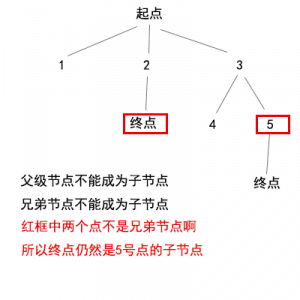
我们过滤无用的直连点越多,程序的性能就会越快,后面的程序会具体的说下这些择优是如何判断
4、哪条路径是最短路径
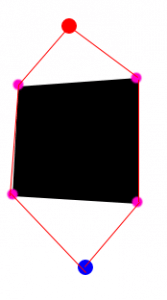
我们都知道了每条路径的每个点,计算一下就知道最短路径了~
再贴演示地址:
http://westanhui.github.io/navigate/index2.html
这里没有开启 debug 了,因为 debug 也没啥好显示的…… 下面是核心程序,完整程序请右键源代码~
|
|
var point = { x: 608, y: 408, index: n, childs: [], parent: {}, isEnd: bool, isObstacle: bool }; |
起点、终点、每个障碍物的点,格式是这样的
x,y 是坐标,isObstacle 是标示是否是障碍物点
index 是索引,其中 start 为-1,end 为-2,障碍物的从 0 开始递增,不要问我为什么-1 和-2…… 拍脑袋
childs 是一个数组,存着该点的可行直连点,并不是直连点哦
注意:存着的对象是深拷贝的!为了方便下面的 parent 属性唯一!
parent 就是该点的父级点,最后用来确定路径的
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
navigate.onclick = function() { outPoint = getPointOutside(obstacles); // 找到障碍物之外的点 if(beforeCheck()) { // 判断起点和终点是否在障碍物内 done(start, {}); showPath(); } }; function done(start, notPoints) { findChild(start, obstacles, notPoints); // 寻找子节点,④ compare(start.childs); // 对子节点进行一次过滤① obstacles[start.index] && (obstacles[start.index].isEnd = true); // 当前的点不再加入子节点寻找② for(var i in start.childs) { if(!avoid[i]) { done(start.childs[i], start.childs); // 递归寻找子节点 } } } function compare(points) { var door = false; for(var i in points) { if(lineStartEnd(points[i], end, obstacles)) { // 是否可以到达终点 console.log('find a path'); console.log(points[i]); globalPath.push(points[i]); avoid[i] = true; // 因为该点已经可以到达终点,所以进行规避③ door = true; } } return door; } |
入口的代码还是很简单的,然后先看①,这里对子节点进行一次过滤,这个过滤就是择优的一种
过滤的机制在于子节点是否可以直接到达终点,比如

图中粉色点已经可以直达终点,那么我们就把它加入 globalPath 这个最终的路径数组,也把它加入到 avoid 这个规避对象里面去,见标记③
然后再看②,isEnd 属性为 true,这就是对已经当过父级的点不再进行可行直连点判断
之前说过一个是父级,还有一个同级的点,都会进行择优过滤,看④
findChild 函数的作用是找寻一个点(第一个参数)的可行直连点,第三个参数传入的就是这个点的同级兄弟节点
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 |
function findChild(p, obstacles, notPoint) { p.childs = Object.create(null); for(var i = 0; i < obstacles.length - 1; i++) { tmp = obstacles[i]; tmpIndex = tmp.index; var door = true; if(notPoint[tmpIndex] || tmp.isEnd) { // 兄弟节点和父级节点直接跳过 continue; } for(var j = 0; j < obstacles.length - 1; j++) { if(tmp.isObstacle) { if(tmp.index === obstacles[j].index || tmp.index === obstacles[j + 1].index) { // ① continue; } } if(p.isObstacle) { if(p.index === obstacles[j].index || p.index === obstacles[j + 1].index) { // ① continue; } } if(isLineCross(p, tmp, obstacles[j], obstacles[j + 1])) { door = false; } if(!door) { break; } } if(door) { var mid = Object.create(null); mid.x = p.x + (tmp.x - p.x) / 2; mid.y = p.y + (tmp.y - p.y) / 2; if(p.isObstacle && tmp.isObstacle) { // ② var diff = Math.abs(tmp.index - p.index); if(diff === 1 || diff === obstacles.length - 2) { p.childs[tmpIndex] = JSON.parse(JSON.stringify(tmp)); p.childs[tmpIndex].parent = p; } } if(isInObstacles(outPoint, mid, obstacles)) { // ③ continue; } p.childs[tmpIndex] = JSON.parse(JSON.stringify(tmp)); p.childs[tmpIndex].parent = p; } } } |
这是整个程序核心的 findChild 函数,第一个 for 循环是依次找每一个点,来判断是否是可行直连点,第二个 for 循环就是具体的判断流程。先看①
假设第一个 for 循环取了一个点 A,要开始判断是否为直连点,然后第二个 for 循环遍历,isLineCross 是判断两条线是否相交的情况,这在上文中也有说过,注意!这里我们需要避免 A 点本身,因为一定是相交,①这里做的判断就是这事
然后再看②
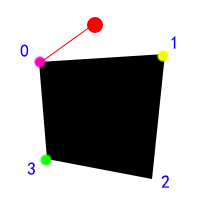
起点和粉色(index 为 0)相连的时候,我们判断粉色点的直连点
1 点和 3 点都是直连点,但是 0-1 线和 0-3 线是相交的,所以我们要考虑到这样的情况,两个点的 index 差为 1,或者为障碍物的首尾
注意函数中有一个 mid 变量还有③这块,这里的作用是判断不相交,因为出现这种情况时
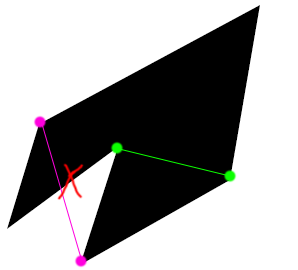
粉色线我们可以通过 isLineCross 判断出来相交,但是绿色线不会,被我们自己①那时的处理给规避掉了
所以这里取了两点中点进行二次验证,是否在障碍物的内部
最后就是计算距离和展示部分
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
function showPath() { // 展示路径 var disArr = []; for(var i = 0; i < globalPath.length; i++) { var arr = []; var tmp = globalPath[i]; arr.push(end); // 先添加终点 arr.push(tmp); // 添加每条路径的最后一个点(达到终点的点) while(tmp.parent) { arr.push(tmp.parent); // 根据点的parent属性往上找到路径上的每个点 tmp = tmp.parent; } arr.push(start); disArr.push({ distance: computeDistance(arr), // 记录距离 path: arr }); } disArr.sort(function(a, b) { // 排序选择最短的路径 return a.distance - b.distance; }); console.log(disArr); drawPath(disArr[0].path); } function computeDistance(arr) { var sum = 0; for(var i = 1; i < arr.length; i++) { sum += Math.sqrt((arr[i].x - arr[i-1].x)*(arr[i].x - arr[i-1].x) + (arr[i].y - arr[i-1].y)*(arr[i].y - arr[i-1].y)); // ① } return sum; } |
这里的代码方便理解,就关注下①,当时我就二了,没有带上 Math.sqrt 自以为可以节省性能,然后就炸了…… 为什么就不用说了吧~不知道的回去问数学老师~~
讲解的都是核心一些的代码,其他的一些请看源代码~如果有疑惑欢迎提出,大家一起交流进步~
总结一下上下两篇文:上文讲解了连线平移的思想,也总结了不好的地方,就是对点和障碍物的位置要求较高,但是对障碍物的形状要求很低,下文要求障碍物的形状为多边形(不过目前来说像素级游戏的障碍物非多边形的很少吧= =,我能想到的也就是圆去做障碍物了……),推荐大家采取下文的方法
结语:总算码完了上下文,累死。在最后多说一句,大部分游戏还是推荐用格子做,因为格子的存在能减少能多事情,或者说减少很多计算量,打比方就是真· 随机生成(并不是标死多个出生点那种随机生成),格子就方便很多。
大家如果有什么想法和 idea 欢迎留言讨论~

















李水军 2020 年 6 月 5 日
有点像是 jump point search, 找到必过点(跳点),再对必过点做 a*判断最短路径。 只是 复杂地形,动态碰撞,如何快速找到必过点? 逐一遍历每个障碍吗?